Persamaan Lingkaran
Baca Juga
Persamaan Lingkaran :
Pusat = ( a,b)
Jari-jari = r
Jika bentuk yang dalam kurung dikuadratkan maka.....
Pusat (P) dan jari-jari r :
Catatan :
dalam menentukan persamaan lingkaran sering digunakan rumus
1. Jarak titik (x1,y1) ke titik (x2,y2) adalah d maka :

2. Jarak titik (p,q) ke garis Ax + By + C = 0 adalah d maka :
Hubungan Lingkaran dengan Garis Lurus
Persamaan garis y = px + q disubtitusikan ke dalam persamaan lingkaran untuk menggantikan variabel y sehingga diperoleh persamaan kuadrat ax2 + bx + c = 0
Hubungan keduanya dapat ditentukan dengan nilai diskriminannya ( D )
Persamaan Garis Singgung Lingkaran
1. Lingkaran ( x - a )2 + ( y - b )2 = r2 dengan gradien garis singgung m
2. Persamaan garis singgung di titik (p,q) pada :
a. Lingkaran ( x - a )2 + ( y - b )2 = r2 adalah :
b. Lingkaran x2 + y2 + Ax + By + C = 0 adalah :
Sketsa Persamaan Lingkaran
Jari-jari lingkaran = r = jarak titik (2,-3) dengan titik (5,7)
sehingga persamaan lingkarannya :
( x - 2 )2 + ( y + 3 )2 = 109
b.
karena menyinggung sumbu y maka jari-jarinya ( r) = absis (x) pusat lingkarannya = 10
sehingga persamaan lingkarannya :
( x - 10 )2 + ( y - 5 )2 = 100
c.

r = jarak titik (-1,-2 ) ke garis 4x + 3y + 5 = 0
sehingga persamaan lingkarannya :
( x + 1 )2 + ( y + 2 )2 = 1
d.
dari sketsa terlihat bahwa titik X pusatnya = titik singgungnya = 5
kemudian dengan memasukkan nilai X = 5 ke persamaan garis y = x - 3 diperoleh nilai Y pusatnya
y = 5 - x = 5 - 3 = 2
sehingga titik pusatnya = (5,2)
karena menyinggung sumbu x maka jari-jarinya ( r) = ordinat (y) pusat lingkarannya = 2
sehingga persamaan lingkarannya :
( x - 5 )2 + ( y - 2 )2 = 4
Pusat = ( a,b)
Jari-jari = r
Jika bentuk yang dalam kurung dikuadratkan maka.....
Pusat (P) dan jari-jari r :
Catatan :
dalam menentukan persamaan lingkaran sering digunakan rumus
1. Jarak titik (x1,y1) ke titik (x2,y2) adalah d maka :

2. Jarak titik (p,q) ke garis Ax + By + C = 0 adalah d maka :
Hubungan Lingkaran dengan Garis Lurus
Persamaan garis y = px + q disubtitusikan ke dalam persamaan lingkaran untuk menggantikan variabel y sehingga diperoleh persamaan kuadrat ax2 + bx + c = 0
Hubungan keduanya dapat ditentukan dengan nilai diskriminannya ( D )
- Jika D > 0 → Persamaan garis berpotongan dengan lingkaran di dua titik
- Jika D = 0 → Persamaan garis bersinggungan dengan lingkaran
- Jika D < 0 → Persamaan raris tidak berpotongan/bersinggungan dengan lingkaran
Persamaan Garis Singgung Lingkaran
1. Lingkaran ( x - a )2 + ( y - b )2 = r2 dengan gradien garis singgung m
2. Persamaan garis singgung di titik (p,q) pada :
a. Lingkaran ( x - a )2 + ( y - b )2 = r2 adalah :
b. Lingkaran x2 + y2 + Ax + By + C = 0 adalah :
Sketsa Persamaan Lingkaran
Seringkali untuk menyelesaikan suatu persamaan lingkaran diperlukan kemampuan untuk menggambarkan sketsanya sehinggga gambaran mengenai persamaan lingkaran tersebut menjadi lebih jelas dan mudah difahami.
Coba perhatikan penyelesaian soal - soal persamaan lingkaran di bawah ini :
Tentukan persamaan lingkaran yang :
a. berpusat di (2,-3) dan melalui titik (5,7)
b. berpusat di (10,5) dan menyinggung sumbu y
c. berpusat di (-1,-2) dan menyinggung garis 4x + 3y + 5 = 0
d. pusatnya pada garis y = x - 3 dan menyinggung sumbu x di titik (5,0)
Jawab :
a.
Jari-jari lingkaran = r = jarak titik (2,-3) dengan titik (5,7)
sehingga persamaan lingkarannya :
( x - 2 )2 + ( y + 3 )2 = 109
b.
karena menyinggung sumbu y maka jari-jarinya ( r) = absis (x) pusat lingkarannya = 10
sehingga persamaan lingkarannya :
( x - 10 )2 + ( y - 5 )2 = 100
c.

r = jarak titik (-1,-2 ) ke garis 4x + 3y + 5 = 0
sehingga persamaan lingkarannya :
( x + 1 )2 + ( y + 2 )2 = 1
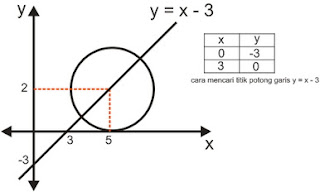
d.
dari sketsa terlihat bahwa titik X pusatnya = titik singgungnya = 5
kemudian dengan memasukkan nilai X = 5 ke persamaan garis y = x - 3 diperoleh nilai Y pusatnya
y = 5 - x = 5 - 3 = 2
sehingga titik pusatnya = (5,2)
karena menyinggung sumbu x maka jari-jarinya ( r) = ordinat (y) pusat lingkarannya = 2
sehingga persamaan lingkarannya :
( x - 5 )2 + ( y - 2 )2 = 4
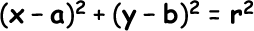












0 Response to "Persamaan Lingkaran"
Post a Comment